In the branch of mathematics known as set theory, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph ().
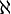The cardinality of the natural numbers is (aleph-null, also aleph-naught or aleph-zero) the next larger cardinality is aleph-one , then and so on. Continuing in this manner, it is possible to define a cardinal number 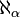for every ordinal number α, as described below.
The concept goes back to Georg Cantor, who defined the notion of cardinality and realized that infinite sets can have different cardinalities.
The aleph numbers differ from the infinity (∞) commonly found in algebra and calculus. Alephs measure the sizes of sets; infinity, on the other hand, is commonly defined as an extreme limit of the real number line (applied to a function or sequence that "diverges to infinity" or "increases without bound"), or an extreme point of the extended real number line. While some alephs are larger than others, ∞ is just ∞.

Aleph-null
is the cardinality of the set of all countable ordinal numbers, called ω₁ or Ω. Note that this ω₁ is itself an ordinal number larger than all countable ones, so it is an uncountable set. Therefore is distinct from . The definition of implies (in ZF, Zermelo-Fraenkel set theory without the axiom of choice) that no cardinal number is between and . If the axiom of choice (AC) is used, it can be further proved that the class of cardinal numbers is totally ordered, and thus is the second-smallest infinite cardinal number. Using AC we can show one of the most useful properties of the set Ω: any countable subset of Ω has an upper bound in Ω. (This follows from the fact that a countable union of countable sets is countable, one of the most common applications of AC.) This fact is analogous to the situation in : any finite set of natural numbers has a maximum which is also a natural number; that is, finite unions of finite sets are finite.
Ω is actually a useful concept, if somewhat exotic-sounding. An example application is "closing" with respect to countable operations; e.g., trying to explicitly describe the σ-algebra generated by an arbitrary collection of subsets. This is harder than most explicit descriptions of "generation" in algebra (vector spaces, groups, etc.) because in those cases we only have to close with respect to finite operations — sums, products, and the like. The process involves defining, for each countable ordinal, via transfinite induction, a set by "throwing in" all possible countable unions and complements, and taking the union of all that over all of Ω.

The continuum hypothesis
Conventionally the smallest infinite ordinal is denoted ω, and the cardinal number 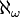is the smallest upper bound of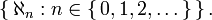

Aleph-ω is the first uncountable cardinal number that can be demonstrated within Zermelo-Fraenkel set theory not to be equal to the cardinality of the set of all real numbers; for any positive integer n we can consistently assume that 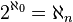, and moreover it is possible to assume 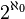is as large as we like. We are only forced to avoid setting it to certain special cardinals with cofinality , meaning there is an unbounded function from to it.

Aleph-ω
To define aleph-α for arbitrary ordinal number α, we must define the successor cardinal operation, which assigns to any cardinal number ρ the next bigger well-ordered cardinal ρ . (If the axiom of choice holds, this is the next bigger cardinal.)
We can then define the aleph numbers as follows


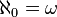
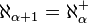
and for λ, an infinite limit ordinal,

The α-th infinite initial ordinal is written ω_α. Its cardinality is written 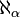. See initial ordinal.

Aleph-α for general α
For any ordinal α we have

In many cases is strictly greater than α. For example, for any successor ordinal α this holds. There are, however, some limit ordinals which are fixed points of the aleph function. The first such is the limit of the sequence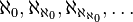

Any inaccessible cardinal is a fixed point of the aleph function as well.

Aleph number in popular culture

Uncountable set
Continuum hypothesis
Beth number